Back to Chapter 1

Optimisation algorithms

Dijkstra & co.

Activity: Traversal reminder

Find the order in which the following nodes are visited in Depth-First Traversal and Breadth-First Traversal

Graph

DFS: A⇒B⇒C⇒D⇒E⇒F
BFS: A⇒B⇒C, (B)⇒D, (B)⇒E⇒F

Traversal vs optimisation

Algorithm optimisations

Algorithm DFS BFS Dijkstra A*
Guaranteed to find any path yes yes
Guaranteed to find shortest path no yes (when nodes have uniform weight)
Efficiently short-circuits irrelevant paths yes (on average) no

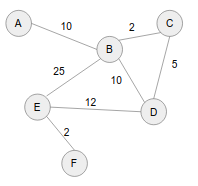
dijkstra's algorithm: Enhanced BFS

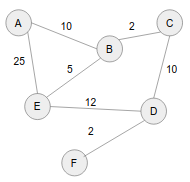
Graph

Activity: user Dijkstra's algorithm to find the best route from A to F

Graph

Algorithm DFS BFS Dijkstra A*
Guaranteed to find any path yes yes yes
Guaranteed to find shortest path no yes (when nodes have uniform weight) yes
Efficiently short-circuits irrelevant paths yes (on average) no yes

Exercises

  1. ​

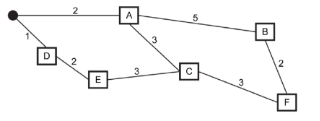
    1. A salesman travels around the country, stopping at specific places, then returning to the starting place.

      Fig. 6.1 shows an example map of places that the salesman visits.

      Fig. 6.1
      Fig. 6.1

      The filled-in circle represents the start and end point. The boxed letters represent the places to visit. The lines are the routs available and the numbers are the length of time each route takes to travel.

    2. The travelling salesman aims to find the shortest route between these places to visit.

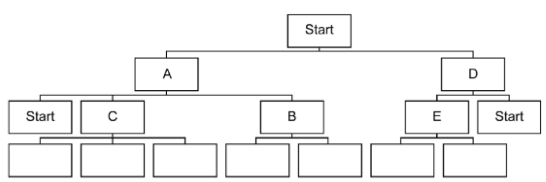
      A programmer is writing an algorithm to solve the travelling salesman problem.

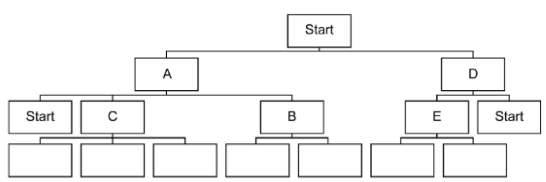
      The programmer is using a tree to find the most efficient route. Fig. 6.2 shows part of the tree with three levels completed.

      Fig. 6.2
      Fig. 6.2

      1. The 'start' nodes on level three are not expanded again as this is a repeat; 'start' has already been expanded.

        Write the place names for the boxes in Fig. 6.2 to complete the fourth level of the tree structure for the map shown in Fig. 6.1

        C⇒{A, E, F}, B⇒{A, F}, E⇒{D, C}

      2. Explain why the tree in Fig. 6.2 is not a binary tree

        It is not a binary tree as there are more than two child nodes for most nodes

    3. The programmer has decided to use a graph instead of a tree structure.

      1. Describe what is meant by a graph structure.

        A graph structure is a group of nodes that are connected to each other, with each connection having a weight that represent the cost of travel between its endpoints

      2. The pseudocode below shows part of an algorithm, which uses a queue to traverse the graph breadth-first.
        Complete the missing elements of the algorithm.

        markAllVertices(notVisited)
createQueue()
start = notVisited[0]
markAsVisited(start)
pushIntoQueue(start)
while QueueIsEmpty() == false
    currentNode = removeFromQueue()
    while allNodesVisited() == false
        markAsVisited(currentNode)
        // following sub-routine pushes all nodes connected to
        // currentNode AND that are unvisited
        pushUnvisitedAdjacents()
    endwhile
endwhile

    4. Fig. 6.3 is a graph representation of the places that the travelling salesman visits. Using this graph, show how Dijkstra's algorithm would find the shortest path from place A to place F

      Fig. 6.3
      Fig. 6.3

      • Step 0
        Visited Queue Unknown
        A - 0
        B - inf
        C - inf
        D - inf
        E - inf
        F - inf
      • Step 1
        Visited Queue Unknown
        A - 0
        A⇒C - 3
        A⇒D - 3
        A⇒B - 5
        E - inf
        F - inf
      • Step 2
        Visited Queue Unknown
        A - 0
        A⇒C - 3
        A⇒D - 3
        A⇒B - 5
        C⇒E - 6
        C⇒F - 6
      • Step 3
        Visited Queue Unknown
        A - 0
        A⇒C - 3
        A⇒D - 3
        A⇒B - 5
        D⇒E - 5
        C⇒E - 6
        C⇒F - 6
      • Step 4
        Visited Queue Unknown
        A - 0
        A⇒C - 3
        A⇒D - 3
        A⇒B - 5
        D⇒E - 5
        C⇒F - 6
        B⇒F - 7
      • Step 5
        Visited Queue Unknown
        A - 0
        A⇒C - 3
        A⇒D - 3
        A⇒B - 5
        D⇒E - 5
        C⇒F - 6
      • Step 6
        Visited Queue Unknown
        A - 0
        A⇒C - 3
        A⇒D - 3
        A⇒B - 5
        D⇒E - 5
        C⇒F - 6
      • Shortest route is A⇒C⇒F