Optimisation algorithms

A*

The A* algorithm uses a heuristic: h = 5(nodes to target)

Add the heuristic value to the sum of the node weights, perform BFS using a priority queue as in Dijkstra's algorithm

Exam style questions

1. ​

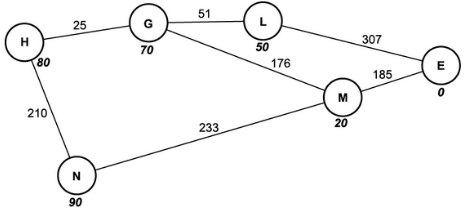
   1. Fig. 2.1 shows the flight paths between a country's airports. The value in bold beneath each node is the heuristic value from E.

      
      Fig. 2.1

      State the full name of the data structure shown in Fig. 2.1.

      • Weighted bidirectional undirected graph

   2. The structure in Fig. 2.1 is searched using the A* algorithm making use of the heuristic values.

      1. State what the heuristic values could represent in Fig. 2.1

         • Physical distance from E to the node

      2. State the purpose of heuristic values in the A* algorithm.

         • Using heuristic values for each node allows the algorithm to spend less time searching paths which are unlikely to be the shortest

      3. Perform an A* algorithm on the data structure in Fig. 2.1 to find the shortest distance between H and E. Show each step of the process, and the calculations performed for each node visited.

         • Step 0

           Visited	Queued	Unknown
           	H - 0 + 80 - 0
           		G
           		N
           		L
           		M
           		E

         • Step 1

           Visited	Queued	Unknown
           H - 80 - 0
           	H⇒G - 0 + 25 + 70 - 0 + 25
           	H⇒N - 0 + 210 + 90 - 0 + 210
           		L
           		M
           		E

         • Step 2

           Visited	Queued	Unknown
           H - 0 - 0
           H⇒G - 95 - 25
           	H⇒N - 300 - 210
           	G⇒L - 25 + 51 + 50 - 25 + 51
           	G⇒M - 25 + 176 + 20 - 25 + 176
           		E

         • Step 3

           Visited	Queued	Unknown
           H - 0 - 0
           H⇒G - 95 - 25
           G⇒L - 126 - 76
           	G⇒M - 221 - 201
           	H⇒N - 300 - 210
           	L⇒E - 76 + 307 + 0 - 76 + 307

         • Step 4

           Visited	Queued	Unknown
           H - 0 - 0
           H⇒G - 95 - 25
           G⇒L - 126 - 76
           G⇒M - 221 - 201
           	H⇒N - 300 - 210
           	L⇒E - 383 - 383 | M⇒E - 201 + 185 + 0 - 201 + 185

         • Step 5

           Visited	Queued	Unknown
           H - 0 - 0
           H⇒G - 95 - 25
           G⇒L - 126 - 76
           G⇒M - 221 - 201
           H⇒N - 300 - 210
           	L⇒E - 383 - 383 | M⇒E - 386 - 386

         • Step 6

           Visited	Queued	Unknown
           H - 0 - 0
           H⇒G - 95 - 25
           G⇒L - 126 - 76
           G⇒M - 221 - 201
           H⇒N - 300 - 210
           L⇒E - 383 - 383

         • Fastest route: H⇒G⇒L⇒E